Teoremas sin palabras

En las matemáticas formales se parte de ciertos axiomas, que son simplemente aseveraciones que aceptamos como punto de partida, de las cuales derivamos los teoremas, que son verdades adicionales que podemos demostrar a partir de los axiomas, siguiendo las reglas de la lógica.

Por ejemplo, un axioma de la geometría Euclidiana es que dos puntos cualesquiera determinan una línea recta única que contiene a ambos. Un teorema geométrico es el que nos dice que los tres ángulos de un triángulo suman 180 grados.

A veces hay teoremas que no son tan simples de demostrar de manera algebraica, pero que se pueden deducir de un diagrama, en el cual la verdad del teorema “salta a la vista”. A estas demostraciones se les ha llamado “demostraciones sin palabras”, porque el diagrama habla por sí mismo. Veamos algunos ejemplos.

Si sumamos enteros impares sucesivos siempre generamos el cuadrado de algún entero. Por ejemplo

1+ 3 = 4
1 + 3+ 5=9
1+3+5+7=16, etc.

Este teorema lo podemos “demostrar” con el diagrama siguiente:

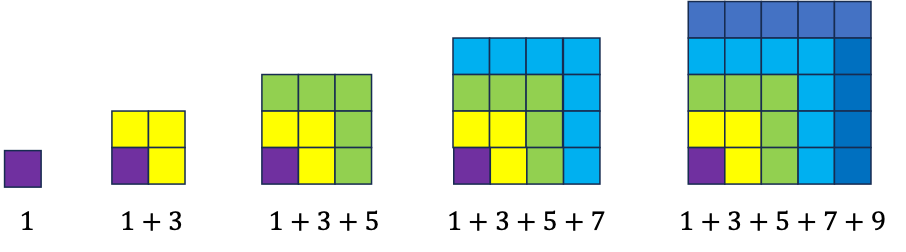
Suma de los enteros impares

Es fácil ver que cada nuevo número de cuadritos de color que agregamos en la esquina derecha superior es un número impar, y que el resultado de la suma del número de cuadritos es un entero al cuadrado.

Un teorema muy famoso es el de Pitágoras, que nos dice que en un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa (el lado más largo). Si llamamos a la longitud de un cateto a, b a la longitud del otro cateto, y c a la hipotenusa, el célebre teorema de la antigüedad clásica dice que:

El siguiente diagrama posiciona un triángulo con esos catetos cuatro veces (dos en naranja y dos en verde), de la forma mostrada a la izquierda. El área c^2 en gris es el cuadrado de la hipotenusa c. Una simple redistribución de los triángulos verdes y naranjas (a la derecha), muestra que el área gris tiene el valor a^2+b^2. De ahí el teorema de Pitágoras.

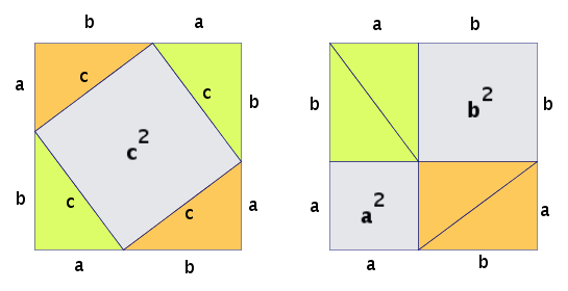
El Teorema de Pitágoras (Wikimedia Commons)

El siguiente teorema parece complicado, pero su realización gráfica es simple. El teorema (para cinco sumandos) dice que:

El teorema se puede generalizar para cualquier número entero n de sumandos y el diagrama que sigue nos muestra el caso especial n=5.

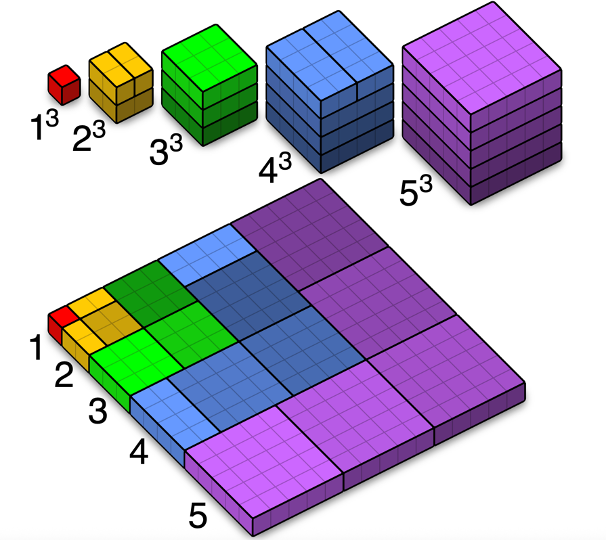
Suma de los cubos de enteros sucesivos (Wikimedia Commons)

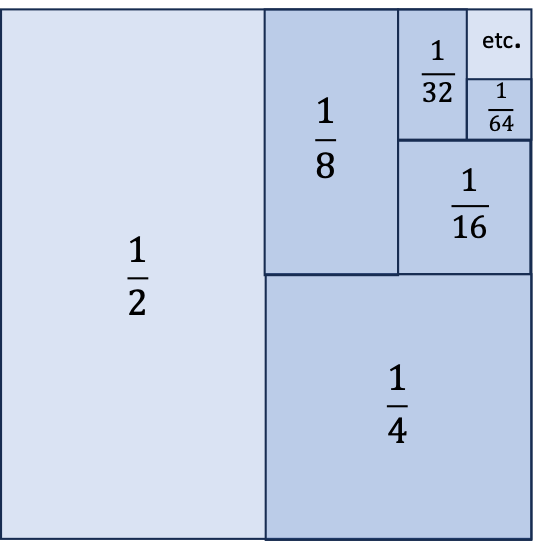
Finalmente, la figura que vemos abajo muestra, utilizando las áreas de rectángulos y cuadrados que se alternan, que

1/2+1/4+1/8+1/16+1/32…etc.=1

El cuadrado más grande tiene lados de longitud 1 (por ello área 1) y la construcción geométrica se prolonga hasta el infinito.