Aritmética de congruencias

Además de la aritmética tradicional, donde tenemos a los números enteros y operaciones con ellos, hay una aritmética alternativa que también utilizamos en la vida diaria. Es la aritmética de congruencias, que utilizamos para operar con el reloj, por ejemplo.

Si un reloj marca las 9 y dejamos pasar cinco horas, llegamos a las 4 (véase diagrama). Podemos decir entonces que 9+5≡2 (módulo 12). Lo que esto quiere decir es que nunca avanzamos más allá del 12, que es la hora cero. Al ir contando las horas pasamos de 9 a 10, y entonces de 10 a 11, a 0, a 1, y finalmente a 2. A la hora 12 la podemos concebir como la hora cero (del amanecer o del atardecer).
 

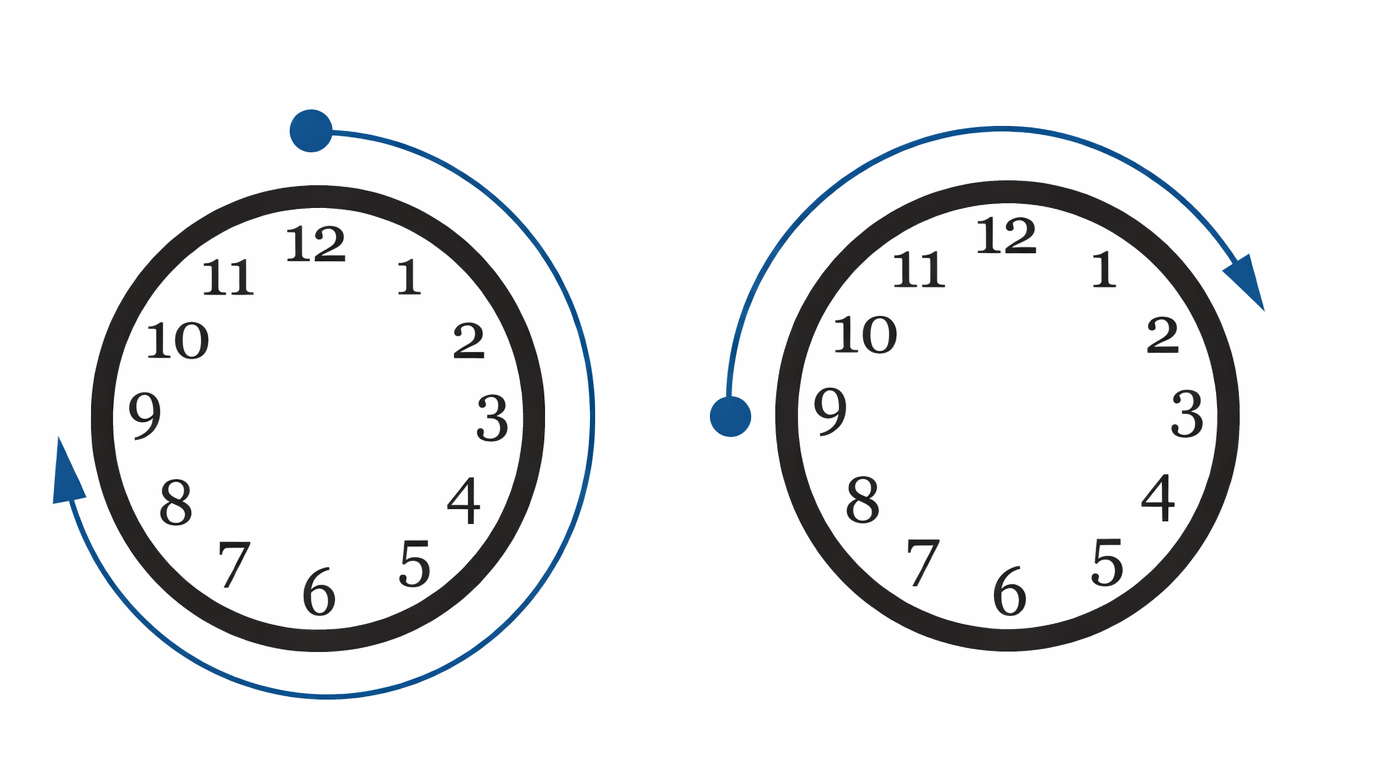
La manecilla del reloj

En la expresión 9+5≡2 (módulo 12) utilizamos las tres barras de congruencia para dejar en claro que no estamos sumando 9 y 5 de manera convencional sino de manera congruencial.

Lo podemos explicar con otro reloj de solo siete horas. Supongamos que el reloj tiene siete posiciones y que las hemos numerado del 0 al 6. Podemos avanzar la manecilla de las horas transmitiéndole impulsos que hacen que rote una posición (un diente) en el sentido convencional de las manecillas del reloj.

Si la manecilla comienza en la posición 0, un impulso la avanza a la posición 1. Un impulso más la avanza a la posición 2, y así sucesivamente, hasta que llegamos a la posición seis. Un impulso adicional regresa a las manecillas a la posición cero y podemos comenzar a contar de nuevo. Como con el reloj usual, pero este solo puede señalar 7 posiciones en vez de 12. Solo podemos contar del cero al seis.

Podríamos pensar que un sistema aritmético como este, con solo siete cifras posibles (de 0 a 6) no es muy útil. Sin embargo, no es así. Ya mostramos que las doce horas del reloj representan un sistema aritmético congruencial con 12 cifras. Y las computadoras, las todopoderosas computadoras, que tantos problemas numéricos resuelven, trabajan con aritmética congruencial.

Lo primero es definir la notación. Cuando decimos que 16≡2 (mod 7), lo que expresamos es que 16 impulsos alimentados al reloj de siete horas, avanzan la manecilla a la posición 2 (es decir, dos vueltas completas más dos horas adicionales). Se puede decir también que 16 y 2 tienen el mismo resto al ser divididos por 7, ya que 16/7=2 con resto 2, y 2/7=0 con resto 2 (en aritmética entera). Similarmente resulta que 18≡3 (mod 15), porque 15 cabe una vez en 18 y el resto es 3. Lo único que realmente hemos hecho es generalizar la aritmética de los relojes para que operen con cualquier número de horas: siete, quince, doce, las que sean.

La aritmética congruencial es interesante porque todos los números poseen lo que llamamos una inversa aditiva. En aritmética de enteros convencionales, sabemos que 2+(-2)=0. En aritmética congruencial no necesitamos a los números negativos. Por ejemplo, 3+4≡0 (mod 7). También 5+2≡0 (mod 7). Podemos decir que 4 es la inversa aditiva de 3 y 2 es la inversa aditiva de 5. Y viceversa, 3 es la inversa aditiva de 4 y 5 es la inversa aditiva de 2 (módulo siete).

Necesitamos los números negativos en la aritmética convencional para poder resolver ecuaciones simples como x+2=5. Lo que hacemos es sumar -2 en ambos lados de la ecuación para obtener como resultado  x =3. En una ecuación sus dos lados son como los dos platos de una balanza. Lo que hacemos en un lado hay que hacerlo en el otro para no perturbar la ecuación.

Lo mismo con ecuaciones de congruencias. Por ejemplo, resolvemos la ecuación

x+5 ≡ 1 (mod 7)

reduciendo el 5 en el lado izquierdo a cero. Para ello sumamos 2 en ambos lados de la ecuación:

x+(5+2) ≡(1+2) (mod 7)

obteniendo

x ≡ 3 (mod 7)

ya que (5+2) ≡ 0 (mod 7).

Un problema con el reloj de doce horas podría ser: ¿Cuántas horas han transcurrido si el reloj comienza en la posición 6 y termina en la posición 3? En términos de una ecuación, la pregunta es:
 

x+6 ≡ 3 (mod 12).

Ya que 6 es la inversa aditiva de 6 (módulo 12), tenemos que

x+(6+6)≡(3+6) (mod 12),

que se reduce a

x≡9 (mod 12).

El resultado tiene sentido, el reloj avanza de las seis a las tres en nueve horas.

Lo que hemos visto aquí se generaliza para cualquier módulo. Si el módulo que queremos utilizar es 9, los dígitos posibles son 0, 1, 2, 3, 4, 5, 6, 7, y 8. Las inversas aditivas de cada uno de esos números, respectivamente, son: 0, 8,7,6,5,4,3,2 y 1.

Lo importante de toda esta disquisición es que existen sistemas numéricos finitos, como el sistema módulo siete, que operan con pocos números y que, sin embargo, poseen un álgebra con la que podemos resolver ecuaciones de congruencias, de gran utilidad en la computación y en áreas como la criptografía. La aritmética congruencial abre un sinnúmero de posibilidades.

En aritmética congruencial también podemos multiplicar. Por ejemplo 3×5 (mod 7) es 15 (mod 7), que se reduce a 1. Pero eso es harina de otro costal que reservamos para otro capítulo.